Survey of Astronomy
-- Laboratory
PLANETARY ORBITS AND KEPLER’S LAWS
Wide are the meadows of night,

And daisies are shining there,
Tossing their lovely dews,
Lustrous and fair;
And through these sweet fields go,
Wand'rers 'mid the stars---
Venus, Mercury, Uranus, Neptune, Saturn, Jupiter, Mars.
'Tired in their silver, they move,
And circling, whisper and say,
Fair are the blossoming meads of delight
Through which we stray.
“Wanderers” by Walter de la Mare
I. Objective
Johannes Kepler (1571-1630), a German mathematician and astronomer, was a man on a quest to discover order and harmony in the solar system. He lived at a time when the motions of the planets through space were not well understood: Nicolaus Copernicus had only recently (1543) published his claim that the Sun, not the Earth, was the center of the solar system, and the idea was not well accepted. With years of hard work, and without the benefit of calculus or the Universal Law of Gravitation (both invented by Isaac Newton only in the latter half of the 17th century), Kepler was able to derive three laws that state how the planets move in their orbits around the Sun. In this lab, you will learn about Kepler’s laws of planetary motion, and explore some of their consequences.
You may wish to refer to pages 72-73 in your text.
II. Exercises
Kepler’s
First Law:
The planetary orbits are ellipses, with the Sun
located at one focus.
For this part of the lab, you will work in groups. You will need two pins, a loop of string, a clean sheet of paper, and a piece of cardboard. You will then be shown how to use these materials to draw an ellipse.
Each person in the group will tie their string to make a loop. Each loop should be of slightly different length: start with 15 cm. of string, then perhaps 16 or 14, and so on. Do not make the loop so large that the ellipse you will draw is to large for the paper. Each person in your group should begin by placing their pins 4 cm. apart. After you each draw your first ellipse, compare each others figure. Then move one of your pins to make the distance between the two pins a little larger, then draw another ellipse. Again, compare with your group members. Repeat this and draw a third ellipse.
a.)
Use the equipment
provided to carefully draw an elliptical orbit on your piece of paper.
The positions of your pins are called the foci (singular: focus) of the ellipse. Next, get a new sheet of paper and draw a single, perfectly drawn ellipse that is nearly circular.
b.)
Label one
focus as the Sun, and the other as the secondary focus.
c.)
The point in
the orbit furthest away from the Sun is called the “aphelion.” The closest point is called the
“perihelion.” Label these positions in
your orbit.
d.)
Label these
parts of your ellipse.
e.)
Measure the
major axis in centimeters and record the length here: _______.
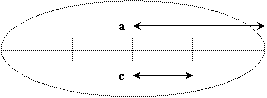
An important parameter of an ellipse is the eccentricity (e). It can be found via the following formula:
e = c/a,
where c is half the distance between the foci (here, your tack marks), and a is the semimajor axis.
f.)
Measure c
and a (in cm), and find the eccentricity of your ellipse. Compare your value of e with those obtained
by the other two students in your group.
Comment on the relation between the eccentricity of an ellipse and its
shape.
g.)
For an orbit
with e=0, what would the value of c be?
How would you place the tacks in order to draw such an orbit? What would
the orbit look like, and what would the semimajor axis (a) be called?
h.)
Look at the
Solar System Data Table near the end of this lab. Which planet’s orbit is the most
eccentric? Which is the most circular?
i.)
Choose three
points at random on the perimeter of your ellipse (which could be three
possible locations of the planet during its orbit). Label these points X,Y,
and Z. Fill in the following table.
Distance from Distance from point Total
Sun
to point (cm)+
to 2nd focus (cm) = Distance (cm)
Point X: + =
Point Y: + =
Point Z: + =
What do you notice? And where
have you seen the numbers in the last column before?
Most of the planetary orbits have quite small eccentricities, which is one of the reasons why they are often called circular. However, the orbits of comets may be much more eccentric.
Kepler’s
Second Law:
The line between a planet and the Sun
(called the “radius vector”) sweeps out equal areas in equal times.
The orbit of the imaginary Comet Frosty is shown on the last page of this lab. Comet Frosty travels around the Sun once in exactly 100 years. It will be at perihelion in the year 2000.
In this section of the lab, you will predict where in its orbit the comet will be at the following times:
2000,2010,2020,2030,2040,2050,2060,2070,2080,2090,2100.
j.)
According to
Kepler’s Second Law, how will the area swept out by Frosty’s radius vector
between 2000 and 2010, compare to the area swept out…
·
between 2010 and
2020?
·
between 2050 and
2060?
·
Between
any two adjacent years in the above list?
Explain your reasoning in detail.
k.)
Fill in the first column of the following table,
using Kepler’s Second Law:
Year Percentage of ellipse’s total Position angle of Frosty
area swept out by Frosty’s (measured counterclockwise
radius vector since year 2000 from perihelion) – in degrees
See j.) above. See
Comet Frosty Table.
2000
2010
2020
2030
2040
2050
2060
2070
2080
2090
2100
The areas swept out by the radius vector fix the position of the comet in its orbit. But how do we measure these areas? It’s not as easy as you might think; there is no simple equation for the area of a swept-out elliptical sector.
In order to plot the position of the comet, we would like to know how these swept-out areas relate to the position angle of the comet (the angle perihelion—Sun—comet, measured counterclockwise from perihelion). The Comet Frosty Table near the end of this lab will tell you just that.
l.)
Fill in the last
column of the table in part k, using the Comet Frosty Table at the end of the
lab, and selecting only the position angles appropriate to the years listed in
part k. Then, with a protractor to
measure the position angles, plot the positions of the comet as it orbits the
Sun. Label these positions with the corresponding
years.
m.)
Does the
comet always travel at the same speed?
If not, at what
position in its orbit does it travel fastest?
slowest?
Kepler’s Third Law:
The square of the orbital period is
proportional to the cube of the semimajor axis:
p2
= a3
(where P is
measured in years, and a is measured in A.U.)
Semimajor axis (a): This was defined at the beginning of this lab. Sometimes a planet is closer to the Sun that this distance, and sometimes it is farther away, but the semimajor axis is the average distance from the Sun. For the Earth, a = 1 A.U. by definition.
Orbital period (P): This is the amount of time that it takes for the planet to go once around the Sun. For the earth, this time is one year.
You can see that for Earth, Kepler’s Third Law works (p = 1, a = 1, 12 = 13).
n.)
If the
Earth’s orbit had a semimajor axis of 2 A.U., how long would it take to go
around the Sun? Use Kepler’s Third Law
to find out, and show your work.
o.)
Choose one
planet other than the Earth, and look up its semimajor axis in the Solar System
Data Table. Plug this value into
Kepler’s Third Law, and calculate what the orbital period should be. How does this compare with the value of P
given in the table?
p.) Choose
one planet other than the Earth and the one you chose in part o. Look up its orbital period. Using Kepler’s Third Law, calculate what the
semimajor axis should be. How does this
compare to the value of a given in the table?
Halley’s Comet travels around the Sun in a highly elliptical orbit (e=0.967). It most recently passed through our neck of the woods in 1986, but it was not very bright, so you might have missed it. Fortunately, it will be back, although not until the year 2062.
q.)
What is the
semimajor axis of Halley’s Comet’s orbit in A.U.?
r.)
How close to
the Sun is Halley’s Comet at perihelion (in A.U.)?
How far away from the Sun is it at aphelion (in A.U.)?
Explain in detail the reasoning by which you obtained these answers,
and show all work.
(Hint: To solve this problem, you need both e and a. It might help to draw a sketch of Halley’s
orbit around the Sun).
s.)
When
Halley’s Comet is furthest from the Sun, it lies just beyond the orbit of which
planet? (See the Solar System Data
Table).
t.)
Reflect on
the ideas presented in this lab. Write a
paragraph conclusion that summarizes the points of the lab, the overall impact
of Kepler’s contributions to astronomy, and how these ideas have impacted the
way you view the universe.
Solar System Data Table
The following is a table of measured orbital parameters for the nine planets of our Solar System.
Name Orbital Period Semimajor Axis
(Earth Years) (Astronomical Units) Eccentricity
Mercury 0.241 0.387 0.206
Venus 0.615 0.723 0.007
Earth 1.000 1.000 0.017
Mars 1.881 1.524 0.093
Jupiter 11.87 5.205 0.048
Saturn 29.63 9.576 0.056
Uranus 84.67 19.28 0.050
Pluto 251.9 39.88 0.253
Comet Frosty Table
Position angle Percent of total Position angle Percent of total
(measured from area swept out (measured from area swept out
perihelion by radius vector perihelion by radius vector
in degrees) since year 2000 in degrees since year 2000
0 0.00% 180 50.00%
5 0.05% 185 59.52%
10 0.10% 190 68.18%
15 0.15% 195 75.45%
20 0.20% 200 81.18%
25 0.26% 205 85.54%
30 0.31% 210 88.78%
35 0.37% 215 91.18%
40 0.43% 220 92.96%
45 0.50% 225 94.29%
50 0.57% 230 95.31%
55 0.64% 235 96.09%
60 0.72% 240 96.70%
65 0.81% 245 97.18%
70 0.91% 250 97.57%
75 1.02% 255 97.89%
80 1.14% 260 98.15%
85 1.28% 265 98.37%
90 1.44% 270 98.56%
95 1.63% 275 98.72%
100 1.85% 280 98.86%
105 2.11% 285 98.98%
110 2.43% 290 99.09%
115 2.82% 295 99.19%
120 3.30% 300 99.28%
125 3.91% 305 99.36%
130 4.69% 310 99.43%
135 5.71% 315 99.50%
140 7.04% 320 99.57%
145 8.82% 325 99.63%
150 11.22% 330 99.69%
155 14.46% 335 99.74%
160 18.82% 340 99.80%
165 24.55% 345 99.85%
170 31.82% 350 99.90%
175 40.48% 355 99.95%
180 50.00% 360 100.00%