Single Source, Shortest Path Algorithms

Definitions

(This all assumes that we're given a graph G = (V, E) and a weight function w : e → R)

• path:  A list of vertices showing how to get from 1 vertex to another in the graph. 
  We're really interested in the edges, but the list of vertices imply the list of edges between them
• weight of a path: the sum of the weights of the edges on a path \(w(p) =\sum\limits_{i=1}^k w(v_{i-1}, v_{i}) \)
• shortest path weight of a path from u to v:
  \[d(u,v) =\left\{ \begin{array}{ll} min(p): w(p): \{p \textrm{ is a path from u} \to v \} \textrm{(if at least one path exists)} \\ \infty, \textrm{if there is no path} \end{array} \right.\]
• shortest path: is any path such that w(p) = d(p) and p exists
• cycle: a cycle is any path that starts and ends in the same place.   So ABCDA is a cycle.
  Note that paths can (poentitally) contain cycles.  ABCDEFCGH contains the cycle CDEFC.

Shortest Path for Unweighted Graphs

For unweighted graphs we can just use BFS to find the shortest path from the source node to any other node.

Shortest Path for Weighted Graphs

Problem: Given G = (V, E) and src ∈V, find a shortest path p (from src to v, ∀v ∈V)

A couple of important notes:

1. Optimal Substructure:
   A shortest path from src to v is composed of subpaths that are also the shortest subpath.
   Given a shortest path: pick any point on it (let's name it t).  The path from src to t is a shortest path from src to t.
   1. This is important because both greedy algorithms and dynamic algorithms exploit this optimal substructure property to to come up with good, correct answers.
      
2. Negative weight edges
   In some cases a graph may contain negative edge weights (for example, if the edges represent financial actions, then getting (or giving) money might be represented with negative edge weights.
   In some cases this might not make sense (e.g., when edges represent roads on a map)
   
3. Shortest paths never contain cycles
   If a graph has a cycle with a net negative weight then the shortest path is undefined (because you can keep going around that cycle, and thus reducing the total each time).
   If the graph has a cycle with a net positive weight it would be pointless to follow it (because doing so will increase the total but will not get you any closer to the destination vertex)

Pseudocode - Dijkstra's

<See notes from the  prior lecture>

Note that Dijkstra's algorithm cannot handle negative weight cycles (in contrast to the Bellman-Ford Algorithm, below)

Pseudocode - Bellman-Ford

First, let's define the 'init' method:

Θ( |V| )

Init(G, s)     s.dist = 0     create an array named distances, whose length is |V|          // This will keep track of the current, known, shortest path distance from the source vertex to any other vertex         fill distances with \( \infty \)         change the slot corresponding to the source vertex to be zero     foreach v ∈ V:        v.dist = \( \infty \)        v.parent = null

 

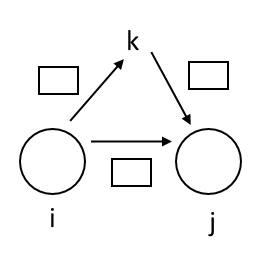
The 'Relax' method will check if the distance from v₁ to v₂ is a shorter way to get to v₂, and if so it will update v₂ so that v₂'s parent/predecessor points back to v₁ (and the distance is updated appropriately).

Θ( 1 )

Relax( Vertex possShortCut, Vertex dest)     maybeShorter = distances[possShortCut] + weight(possShortCut, dest)     if maybeShorter < distances[dest]         distances[dest] = maybeShorter         dest.dist = maybeShorter         dest.parent = possShortCut In the picture below, 'j' is e.destination in the above code 'i' is the current predecessor in the graph before 'j' 'k' is e.start in the above code

Note: Infinity + x is still infinity
The Bellman-Ford algorithm will go through and repeatedly relax all the edges, checking (over and over) to see if there's a shorter path between any of the vertices.

Θ( |V| )	Bellman-Ford(Graph G, Vertex src)    Init(G, src)
Θ(|V| * |E|)	for( i = 1; i ≤ |G.V| - 1; i++ ) // note that we're just counting here - we need to do the inner loop |G.V| times       // think of this as 'best route after 1 hop', then after 2 hops, etc       foreach edge e ∈ G.E  // go through all the edges in the graph.  _ALL_ of them          Relax(e.start, e.destination) // starting from src can we use e.start as a shortcut to get to e.dest?
Θ(|E|)	// lastly, check for negative-weight cycles:     foreach edge e ∈ G.E // e goes from u to v         if( v.dist > u.dist + w(u,v)             return false;
Θ( 1 )  :)	//No negative weight cycles    return true

 

---